Definition:

It is the combination of physical, mathematical, and computer laws and techniques to predict the behavior of solid materials that are subjected to mechanical or thermal loadings. It is the branch of mechanics that deals with the behavior of solid matter under external actions. The external actions may be:

• External Force
• Temperature Change
• Displacement

Applications of Solid Mechanics

This field has a wide range of applications, laws and concepts of solid mechanics are used:

• In Civil Engineering to design foundations and structures
• In Geo-Mechanics to model shape of planets, tectonics and predict earthquakes
• In Mechanical Engineering to design load bearing components for vehicles, power generation and transmission

Some Important Definitions in Solid Mechanics

Stress

When an external force is applied on a body, it undergoes deformation which is resisted by the body. The magnitude of the resisting force is numerically equal to the applied force. This internal resisting force per unit area of the body is known as stress.

• Stress = Resistive Force/Area
• In equation form: σ = P/A,
• Units are
  • – N/m², kN/m² MPa (Mega Pascal)
  • – Psi (lb/in²), psf (lb/ft²)
  • – Ksi (kips/in²), ksf (kips/ft²)

Strain

When a body is subjected to an external force, there is some change of dimension in the body. Numerically the strain is equal to the ratio of change in length to the original length of the body.

• Strain = Change in length/Original length
• In equation form: ε= δL/L
• Units
  • m/m, mm/m
  • In/in, in/ft

Primary Strain/Longitudinal Strain/Direct Strain

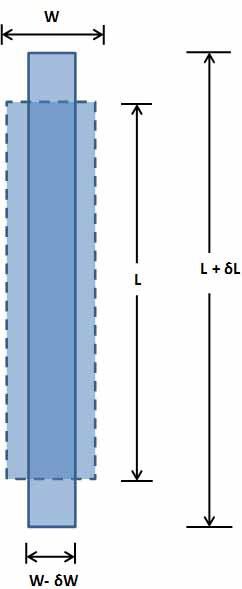It is the ratio of the change in longitudinal length (dimension parallel to the direction of applied force) to the original longitudinal length.

Longitudinal Strain = δL / L

Secondary Strain/Lateral Strain/indirect Strain

It is the ratio of the change in lateral dimension (dimension not parallel to the direction of applied force) to the original lateral dimension.

Lateral Strain = δW / W

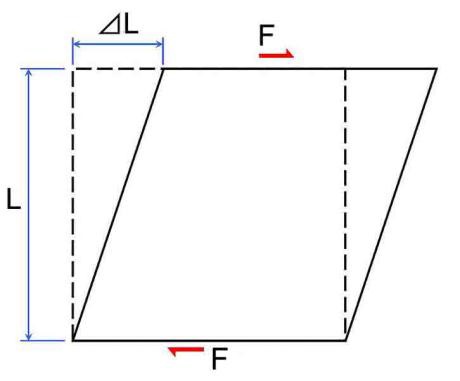
Shear Stress(τ) and Shear Strain(G)

The two equal and opposite forces act tangentially on any cross sectional plane of the body tending to slide one part of the body over the other part. The stress induced is called shear stress and the corresponding strain is known as shear strain.

Hooke’s law

This law states that when a material is loaded, within its elastic limit, the stress is directly proportional to the strain.

Stress α Strain

σ α ε

σ = Eε

E = σ/ε

Its unit is same as that of Stress Where, – E is Young’s modulus – σ is Stress – ε is Strain

Poisson Ratio

It is the ratio of the lateral strain to the longitudinal strain and is constant property of each material. Poisson’ ratio (μ or 1/m) = Lateral strain /Longitudinal strain

Young’s Modulus:

It is the ratio of the normal stress to the normal strain.

E = σ/ε

Rigidity Modulus:

Its is the ratio of the shear stress to the shear strain.

N = Shear stress/Shear strain

N = τ/G

Elastic Limit:

The maximum stress that can be applied to a metal without producing permanent deformation is known as Elastic Limit – When stress is applied on a body its dimensions change, these changes can be reversed if the stress applied do not cross a certain limit. – This certain limit within which the material when unloaded will re-gain its original dimensions is known as Elastic Limit. – Beyond the elastic limit the changes will be permanent and cannot be reversed without an external force. Brittle materials tend to break at or shortly past their elastic limit, while ductile materials deform at stress levels beyond their elastic limit.

Stress-Strain Relation

Yield Point or Yield Stress

It is the lowest stress in a material at which the material begins to exhibit plastic properties. Beyond this point an increase in strain occurs without an increase in stress which is called Yielding.

Ultimate Strength

It is the maximum stress that a material can withstand while being stretched or pulled before necking.

Strain Hardening

It is the strengthening of a metal by plastic deformation because of dislocation (irregular) movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and alloys can be strengthened by this method.

Strain Energy:

Whenever a body is strained, some amount of energy is absorbed in the body. The energy that is absorbed in the body due to straining effect is known as strain energy.

Resilience:

The total strain energy stored in the body is generally known as resilience.

Proof Resilience:

The maximum strain energy that can be stored in a material within elastic limit is known as proof resilience.

Modulus of Resilience

It is the ratio of the proof resilience of the material to the unit volume • Modulus of resilience = Proof resilience /Volume of the body.